ON17 P52 Q2 Standing Waves

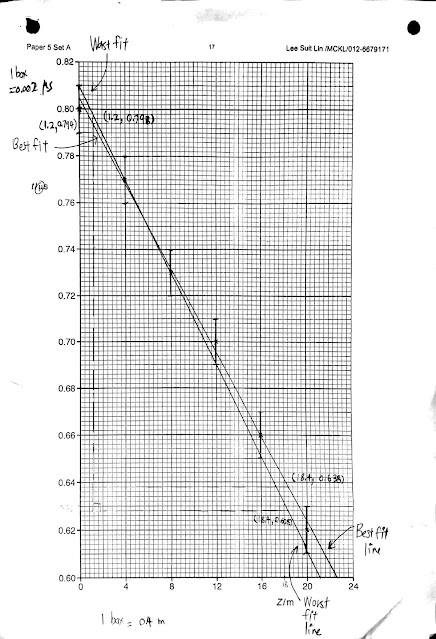
 9702/52/O/N/17: A student is investigating stationary waves on a stretched elastic cord. A vibrator attached to the cord is connected to a signal generator. The apparatus is set up as shown in Fig. 2.1.

The  mass  M  attached  to  the  cord  is  adjusted  until  resonance  is  obtained.  The  number  n  of  antinodes on the stationary wave is recorded. The experiment is repeated with different masses to obtain different values of n. It is suggested that M and n are related by the equation

\(f = \dfrac{n}{2L} \sqrt{\dfrac{Mg}{\mu}} \)

where f  is  the  frequency  of  the  vibrator,  g  is  the  acceleration  of  free  fall,  L  is  the  length  of  the  elastic cord and n is the mass per unit length of the elastic cord.

 

October/November 2017 Paper 5 Variant 2 Question 2 data analysis.

ON17 P51 Q2 Force on Bridge

9702/51/O/N/17:  A student is investigating how the forces acting on a bridge vary as the position of a load on the bridge is changed. The bridge is modeled as shown in Fig. 2.1 with two newton-meters providing the support forces. 

 A load of mass m is placed at a distance x from support A. The readings of the newton-meters T1 and T2 are recorded for different values of x.

It is suggested that T1, T2 and x are related by the equation 

\( T_1 - T_2 = \dfrac{mg(s - x) - mgx}{s} \)

where s is the separation of the newton-meters and g is the acceleration of free fall.

Oct/Nov 2017 Paper 5 Variant 1 Questions 2 data analysis.

MJ17 P51 Q2 Oscilloscope Pulse

9702/51/M/J/17: A student is investigating how the time for an electrical pulse to travel in a coaxial cable varies with the length of the cable. The pulse is reflected at one end of the cable. An oscilloscope is used to display the initial pulse and the reflected pulse. The trace on the oscilloscope is shown in Fig. 2.1.

The time t for the pulse to travel to the end of the cable and back is determined by measuring the distance d between the pulses on the screen, and then using the time-base and the relationship t = d × time-base. The initial length of the cable is L. A total length Z is removed from the cable and the experiment is repeated. It is suggested that t and Z are related by the equation v = 2 (L – Z)/t where v is the speed of the pulse.

Solutions for practical Paper 5 variant12 Question 2 May/June 2017 Cambridge A Level Physics.